Chaotic dynamics of an individual memristor demonstrated
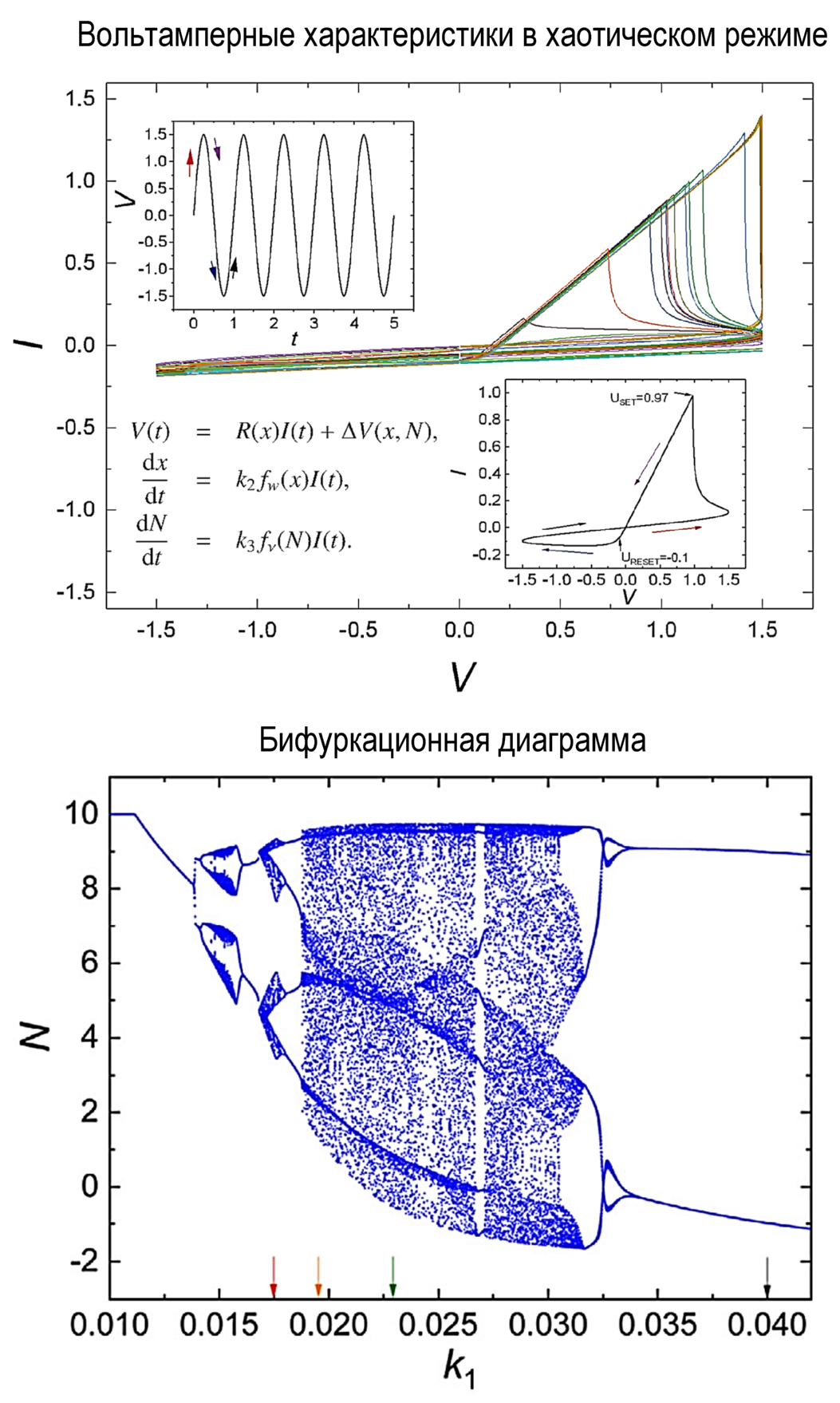
Current-voltage characteristics in the chaotic regime
Bifurcation diagram
Lobachevsky University researchers, together with their colleagues from Russia (Research Institute for Molecular Electronics, Zelenograd) and the US (University of South Carolina) have demonstrated for the first time the chaotic dynamics of an individual memristor.
The variability in the characteristics of a memristor device in the experiment is explained by deterministic chaos. The paper summarizing the research results was published in the journal Chaos, Solitons & Fractals (impact factor - 3.764 (Q1), JCR 2019). The research project is implemented at the Stochastic Multistable Systems Laboratory (StoLab) of the UNN Research and Education Center "Physics of Solid State Nanostructures" headed by the leading scientist Prof. Bernardo Spagnolo. It is supported by a megagrant from the Russian Federation Government (Agreement #074-02-2018-330).
Leon Chua, a world-renowned professor at Berkeley and a long-time friend of Lobachevsky University, predicted back in 1971 that a memristor is a "lost" fourth passive element in electrical circuits, which can change its resistance depending on the electrical charge that flows through it (memristor = memory resistor).
This original definition has provoked discussions and disputes, especially since the memristive effect was compared with a resistive switching effect in a simple "metal-oxide-metal" thin-film structure in 2008. Irrespective of this, the generalised definition of a memristor as a dynamic system, which Leon Chua coined in 1976, still holds true.
On the one hand, this universal definition allows us to relate an arbitrary set of dynamic variables at the system level to specific physical and chemical phenomena that are responsible for changing the resistance of the material at the microscopic level. On the other hand, it enables the use of a rich arsenal of nonlinear dynamics methods to interpret and predict the "live" behaviour of real memristive devices as part of brain-like neural network architectures.
These capabilities have been successfully exploited in the new work to describe the complex dynamics of a memristor in a second-order model under external influence. The length of the conductive region (filament) and the charge that accumulates dynamically on the defect centres in the oxide layer are chosen as dynamic variables. The model consists of two autonomous differential equations and one algebraic equation, which depends on an external control provided by a time periodic signal.
Various periodic modes, as well as mixing and chaotic dynamics were obtained in the numerical experiment. Phase diagrams indicating the presence of a chaotic attractor were plotted in the three-parameter space of the model. From the practical point of view, the most interesting result is that the instability of the resistive switching behaviour, which has always been a stumbling block in the way of integrating memristors into traditional electronic circuits, can be interpreted as the manifestation of chaotic dynamics of its internal state variables.



